Dr. Wiebke Salzmann
freie Lektorin und Autorin
Wissenstexte
Physik-Wissen
Korona

Auf dieser Seite erwarten Sie helle Scheiben und bunte Ringe am Himmel.
www.wissenstexte.de > Physik-Wissen > Optik > Beugung > Korona
Korona
(atmosphärische Leuchterscheinung)
Sollte jemandem auffallen, das viele der Bilder hier auch in dem entsprechenden Artikel in der Wikipedia auftauchen – die Bilder (und auch etliches von dem Text) habe ich dort eingestellt.
– Entstehung der Ringe
– Farbreihenfolge
– Beugung an anderen Teilchen
– Einfluss der Wellenlänge
– Einfluss der Tropfengröße
– Bestimmung der Tropfengröße
– Simulationen
– Koronen und das Wetter – Bauernregel
Ein Beispiel für eine Beugungserscheinung oder Interferenzerscheinung sind die Koronen, die man manchmal bei dünner Bewölkung um den Mond sieht. Meist ist nur eine helle Scheibe mit gelb-rötlichem Rand zu sehen, mit etwas Glück beobachtet man jedoch farbige Ringe. Die helle Scheibe im Zentrum heißt Aureole, oft auch Hof genannt. Die Ringe nennt man Korona; in der Alltagssprache heißen sie auch Kränze, was zu Verwirrung führen kann, da auch die sehr viel größeren Halos als Kränze bezeichnet werden. Während Halos durch Brechnung an Eiskörnern entstehen, sind Koronen eine reine Beugungserscheinung.
- Abb. 1 ¦ Aureole um den Mond

- Unterschiedliche Wolkenarten können Aureolen hervorrufen.
- Abb. 2 ¦ Vergleich Korona und Halo

- Zum Vergleich: Halo (oben), Korona (unten). Neben den intensiveren Farben bei der Korona ist vor allem der Größenunterschied auffällig.
Koronen sind meist um den Mond zu beobachten, seltener um die Sonne. Dies liegt jedoch nicht daran, dass sie um die Sonne weniger häufig auftreten, sondern daran, dass das Licht der Sonne die Koronaerscheinung überstrahlt und man darüberhinaus in der Regel den Blick in die Sonne meidet (und wegen der Gefahr für die Augen auch meiden sollte). Zur Beobachtung von Sonnenkoronen muss das Sonnenlicht daher abgeschwächt werden – durch die Verwendung von Filtern oder indem man das Phänomen im Spiegelbild beobachtet, auf einem Gewässer oder einer Fensterscheibe.
Meist ist auch um den Mond nur die Aureole zu sehen – eine weiße Scheibe, deren Rand in Gelb und Rot übergeht. Der Mond selbst wird von der Aureole oftmals überstrahlt. Ist er zu sehen, fällt der Größenunterschied zwischen ihm und der Aureole sofort auf. Während die Scheibe des Vollmonds unter einem Sehwinkel von etwa 0,5° zu sehen ist, erreicht der Durchmesser der Aureole eine Winkelausdehnung von 1,3° bis 4°, je nach Größe der Tropfen. Aureolen findet man mehr oder weniger ausgeprägt in fast allen (nicht zu dicken) Arten von Wolken, weshalb sie vergleichsweise häufig auftreten.
- Abb. 3 ¦ Aureolen

- Aureole um den Mond.
-

- Eine schwache Aureole um die aufgehende Sonne, erzeugt durch dünne Wolken. Diese Aureole habe ich erst auf dem Foto entdeckt, sie ist sichtbar, weil die Sonne noch nicht so hell erscheint.
-
- Aureole um die Sonne im Spiegelbild (im Gartenteich).
Unter günstigen Bedingungen schließen sich an die Aureole farbige Ringe an – mit der Farbreihenfolge (von innen nach außen): blau, grün, gelb, rot. Es wurden bis zu vier Ringsysteme beobachtet. Bei den äußeren fehlt das Blau, ansonsten sind die Farben ähnlich denen im ersten Ringsystem. Koronen können sehr unterschiedliche Ausdehnung haben, der Winkeldurchmesser der äußersten Ringe kann bis zu 15° betragen. Beim Durchzug von Wolken kann sich die Korona verändern – der Durchmesser kann wachsen oder schrumpfen, Ringe erscheinen oder verschwinden wieder, je nachdem, wie sich die Tropfengrößen verändern.
- Abb. 4a ¦ Korona um den Mond
- Abb. 4b ¦ Korona um den Mond
- Wegen der Wolkenlücken kann man hier schön den Größenunterschied zwischen der weißen Scheibe der Aureole und der Mondscheibe erkennen.
- Abb. 4c ¦ Korona um die Sonne
- Korona um die Sonne, als Spiegelung im Dolgener See
Man kann darüber hinaus auch „künstliche“ Koronen beobachten oder erzeugen, indem man beispielsweise durch eine beschlagene Scheibe oder Nebel auf eine Lampe blickt. Auch Staub in der Atmosphäre (nach Vulkanausbrüchen oder durch Pollenflug) kann Koronen verursachen.
- Abb. 5 ¦ Korona um eine Lampe
- Korona um eine Straßenlampe, erzeugt durch eine beschlagene Fensterscheibe.
-
- Korona um eine Stubenlampe, erzeugt durch Nebel.
Die Korona als Beugungsbild einer Kreisblende
Koronen entstehen durch Beugung des Sonnen- oder Mondlichtes an Wassertropfen – es müssen also Wolken vorhanden sein, wenn man eine Korona beobachten will. Diese Wolken dürfen andererseits aber auch nicht zu dick sein, da das Mond- bzw. Sonnenlicht sie durchdringen können muss.
Nach dem Babinetschen Theorem entspricht das Beugungsbild einer Kreisscheibe in guter Näherung demjenigen einer Kreisblende gleichen Durchmessers, welches wiederum annähernd demjenigen einer Kugel entspricht – entscheidend ist die kreisförmige Begrenzung des beugenden Hindernisses. Das durch die Wassertropfen erzeugte Beugungsbild kann also durch dasjenige einer kreisförmigen Lochblende beschrieben werden. (Zum Zustandekommen des Beugungsbildes siehe: Beugung.)
Stellt man einen Schirm hinter die Kreisblende, entsteht ein Beugungsbild aus einem hellen Scheibchen (dem Zentralbild; hier ist die Intensität am größten) und konzentrischen hellen und dunklen Ringen – wobei die Intensität der hellen Ringe nach außen abnimmt. Während das Zentralbild mehr oder weniger der ursprünglichen Ausbreitungsrichtung des Lichtes entspricht (der Ablenkungswinkel liegt um 0°), sind die Ringe um so weiter, je größer der Ablenkungswinkel ist.
Dem Zentralbild entspricht die Aureole, den Beugungsringen die farbigen Ringe um die Aureole.
Der Durchmesser der Beugungsringe hängt vom Durchmesser der Blende beziehungsweise der Scheibe und der Lichtwellenlänge ab. Die Ringe werden umso weiter, je größer die Wellenlänge und je kleiner die Blende oder Scheibe ist – also je kleiner der beugende Wassertropfen in der Wolke ist.
Entstehung von Ringen um den Mond
Bislang wurde das Beugungsbild eines einzelnen Tropfens behandelt und stillschweigend mit der Korona gleichgesetzt. Dass das tatsächlich geht, obwohl sich eine Korona aus den Beugungsbildern vieler Tropfen zusammensetzt, soll nun erläutert werden.
Das Beugungsbild hinter einem Tropfen besteht aus konzentrischen Ringen. Ohne einen Schirm, auf dem diese Ringe erscheinen, muss man sich das Licht als in Kegelmäntel hineingebeugt vorstellen (Abb. 6). Die Beugungsringe erhält man, wenn man einen Schirm in diesen Kegel stellt – man sieht sie dort, wo der Schirm den Kegel schneidet.
- Abb. 6 ¦ Entstehung der Ringe I
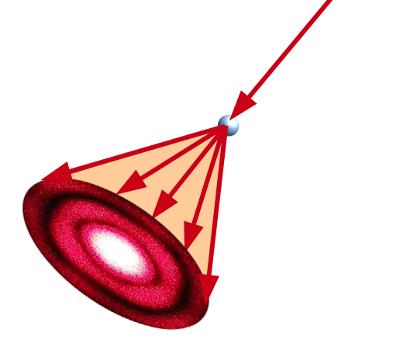
- Die Beugungsringe sind die Schnittlinien der Kegelmäntel mit der Ebene des Schirms. Es gehört natürlich zu jedem Ring ein Kegelmantel, aber das wäre nicht mehr übersichtlich darstellbar gewesen.
Zur Entstehung einer Korona sind zwar sehr viele solcher Wassertropfen erforderlich; jedoch wird jeder Lichtstrahl im Mittel nur an einem Tropfen gebeugt, weil die Tropfen in den Wolken recht große Abstände voneinander haben. Zunächst erzeugt also jeder Tropfen sein eigenes Beugungsbild bzw. seine eigenen Kegelmäntel gebeugten Lichtes. Von dem Licht, das von einem Tropfen gebeugt wird, kann jedoch nur dasjenige vom Beobachter wahrgenommen werden, welches in sein Auge fällt. Das Licht etlicher Kegelmäntel wird man deshalb gar nicht sehen, weil deren Licht am Auge vorbeiläuft (hellrote Pfeile in Abb. 7). Die Kegelmäntel, deren Licht man wahrnimmt, haben alle denselben Öffnungswinkel (einheitliche Tropfengröße vorausgesetzt). Deshalb kommt das Licht, das man wahrnimmt, aus einen kreisförmigen Gebiet um die Lichtquelle.
- Abb. 7 ¦ Entstehung der Ringe II
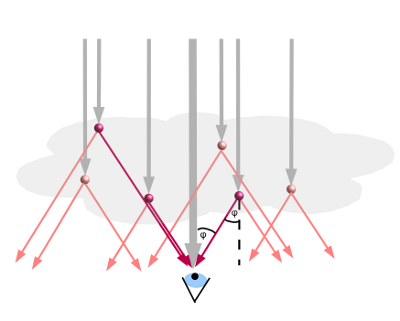
- Die Korona wird von dem Licht erzeugt, das ins Auge fällt (dunkelrote Pfeile). Entscheidend für die Ausdehnung der Ringe ist der Sehwinkel: Die dunkelroten Tropfen sollen das rote Licht so beugen, dass bei einem Ablenkwinkel φ ein Maximum entsteht. Gleichzeitig sollen sich die dunkelroten Tropfen an einer Position befinden, dass das um φ abgelenkte rote Licht ins Beobachterauge trifft (dunkelrote Pfeile). Der Beobachter sieht also an der Stelle der dunkelroten Tropfen rotes Licht. Und zwar unter einem Sehwinkel von ebenfalls φ (Ablenkwinkel und Sehwinkel sind gleich, weil es Wechselwinkel sind.) Die Höhe des Tropfens oberhalb des Beobachters spielt dabei keine Rolle, er sieht beide dunkelroten Tropfen auf der linken Seite unter demselben Sehwinkel (gleiche Tropfengröße vorausgesetzt), d. h., beide haben scheinbar denselben Abstand vom Mittelpunkt der Aureole. Beide sind für den Beobachter also Bestandteil des roten Ringes.
- Abb. 8 ¦ Entstehung der Ringe III
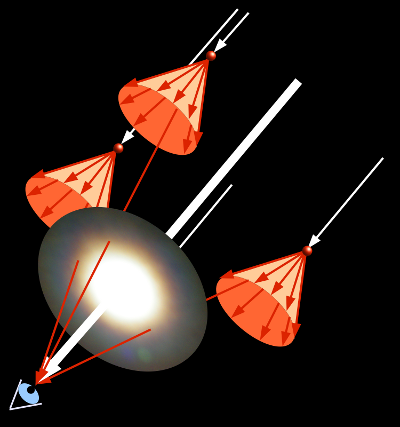
- Um einen vollständigen Ring zu erhalten, muss Abb. 7 um die Ausbreitungsrichtung gedreht werden.
Entstehung der Farbreihenfolge
Auch die Farbreihenfolge lässt sich auf diese Weise veranschaulichen. Zunächst wird ein weit außen liegender Tropfen betrachtet, der rotes und blaues Licht beugt. Das rote Licht wird stark gebeugt (siehe Einfluss der Wellenlänge) und gelangt somit ins Auge des Beobachters. Das blaue Licht wird weniger stark gebeugt und geht deshalb außen am Beobachterauge vorbei. Nun nehmen wir einen Tropfen, der weiter innen liegt. Das rote Licht, das von diesem gebeugt wird, trifft nicht ins Auge, sondern geht innen vorbei. Statt dessen gelangt nun das blaue, schwächer gebeugte Licht ins Auge des Beobachters. Von den außen liegenden Tropfen nimmt der Beobachter also das rote, von den innen liegenden das blaue Licht wahr. Er sieht deshalb innen einen blauen Ring, außen einen roten.
- Abb. 9 ¦ Farbreihenfolge I
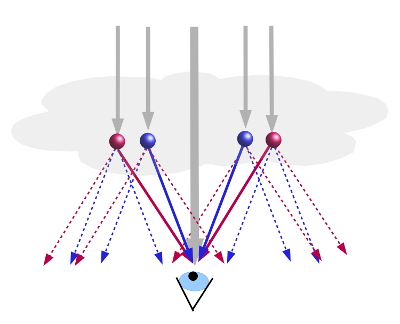
- Die Kegelmäntel blauen Lichtes haben einen kleineren Öffnungswinkel, treffen das Auge also unter einem kleineren Sehwinkel. Durch gestrichelte Pfeile dargestelltes Licht trifft nicht ins Auge.
- Abb. 10 ¦ Farbreihenfolge II
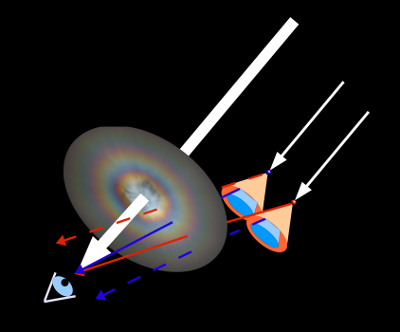
- Das blaue Licht, das ein Beobachter wahrnimmt, kommt von weiter innen liegenden Tropfen als das rote.
Beugung an anderen Teilchen
Es müssen nicht Wassertropfen sein, die das Licht beugen – auch wenn dies bei den weitaus meisten Koronen der Fall ist. Auch Pollenkörner, Aerosole (wie beispielsweise nach Vulkanausbrüchen) oder Eiskristalle kommen in Frage. Zwar haben Eiskristalle keine Kugelform, sondern erzeugen als langgestreckte Nadeln das Beugungsbild eines Spaltes, da die Eisnadeln aber völlig unregelmäßig in den Wolken ausgerichtet sind, addieren sich die Linien der Spalt-Beugungsbilder zu Ringen. Pollenkoronen dagegen können ellipsen- oder rautenförmig sein, da Pollen oftmals eine bestimmte Ausrichtung bevorzugt einnehmen. Nach Vulkanausbrüchen findet sich viel Staub in der Atmosphäre, der ebenfalls Koronen hervorrufen kann. Da diese Aerosole mit 2–3 μm Durchmesser eine geringere Ausdehnung haben, ist die Aureole entsprechend größer, nämlich 13°–20°, Winkel von bis zu 30° wurden beobachtet. Sie werden Bishopsche Ringe genannt, nach S. E. Bishop, der sie 1883 nach dem Ausbruch des Vulkans Krakatau erstmals beschrieben hat.
- Abb. 11 ¦ Korona mithilfe von Bärlappsporen

- In einem Experiment lassen sich Koronen erzeugen, indem man eine Glasscheibe mit Bärlappsporen bestäubt und diese von hinten beleuchtet. Um die Erscheinung fotografieren zu können, musste ich das helle Zentralbild überkleben, es hätte sonst alles überstrahlt.
Einfluss der Wellenlänge
Der Ringdurchmesser ist von der Wellenlänge des Lichtes abhängig – je größer die Wellenlänge, desto stärker die Beugung, d. h., desto größer die Ablenkung des Lichtes aus der ursprünglichen Richtung.
Das Hauptmaximum liegt für alle Wellenlängen im Zentrum (um den Ablenkwinkel 0°), weshalb sich hier alle Farben zu Weiß überlagern und eine weiße Aureole erzeugen. Allerdings liegen die 1. Minima für jede Wellenlänge bei einem anderen Ablenkwinkel – blaues Licht hat den kleinsten, rotes den größten Ablenkwinkel. Die Hauptmaxima für gelbes und rotes Licht ragen also über den Bereich hinaus, indem alle Farben zusammen Weiß ergeben, das blaue Hauptmaximum dagegen verschwindet im Weiß. Deshalb entsteht auf den ersten Blick der Eindruck, die Farbreihenfolge in der Korona beginne mit Rot. Wie oben festgestellt, beginnt sie jedoch mit Blau.
Die Nebenmaxima haben ebenfalls für jede Wellenlänge eine andere Position. Da rotes Licht eine größere Wellenlänge hat als blaues, wird es stärker gebeugt und bildet daher Ringe mit größerem Durchmesser als das blaue Licht. Das ursprünglich weiße Mond- oder Sonnenlicht wird auf die Weise durch die Beugung aufgespalten und es bilden sich die farbigen Ringe. Neben der Farbigkeit an sich erklärt dies auch die Reihenfolge der Farben von Blau über Grün und Gelb nach Rot – das stärker gebeugte rote Licht erzeugt weiter außen ein Helligkeitsmaximum, weshalb der rote Ring weiter außen liegt als der blaue (Abb. 9 und 10).
Nach der Beugungstheorie lässt sich die Intensität in Abhängigkeit vom Ablenkwinkel mit folgender Gleichung berechnen:
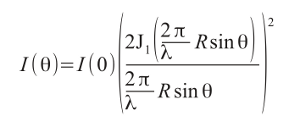 (1)
(1)
In der Gleichung bezeichnen: I = Intensität; λ = Wellenlänge; θ = Ablenkwinkel (sorry, in Abb. 7 wird der Ablenkwinkel mit φ bezeichnet); R = Radius des beugenden Hindernisses (hier also der Tropfenradius); J1 = Besselfunktion 1. Art und 1. Ordnung.
Für die Positionen der ersten Minima findet man für: 440 nm (blau): ca. 1,5°; 650 nm (rot): ca. 2,3°; für die der ersten Nebenmaxima: 440 nm (blau): ca. 2°, 650 nm (rot): ca. 3°.
- Abb. 12 ¦ Einfluss der Wellenlänge
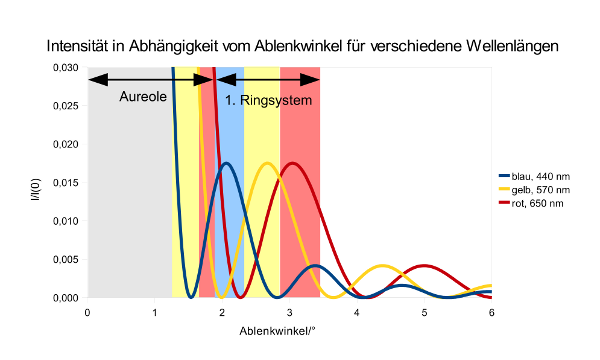
- Es sind die Intensitäten des gebeugten Lichtes in Abhängigkeit vom Ablenkwinkel für verschiedene Wellenlängen und einen Tropfenradius von 10 μm dargestellt. Die Intenesitäten sind durch die Intensität des Hauptmaximums I(0) dividiert. Es sind drei Kurven für rotes, gelbes und blaues Licht dargestellt. Ein Maximum einer Kurve bedeutet auch ein Maximum in der Intensität des jeweiligen Lichtes. Die Hauptmaxima ragen über die Darstellung hinaus, sie ergeben die Aureole. Die ersten Nebenmaxima ergeben das erste Ringsystem.
Meist wird nur ein Ringsystem beobachtet, nur mit Glück sieht man mehrere. Das liegt daran, dass die Nebenmaxima der verschiedenen Wellenlängen mit zunehmender Ordnung breiter werden und deshalb immer stärker übereinanderfallen, d.h., die Farben mischen sich mehr und mehr zu Weiß, und zudem nimmt die Intensität rasch ab.
Experiment zum Einfluss der Wellenlänge
Den Einfluss der Wellenlänge kann man auch im „heimischen Labor“ untersuchen. Statt einer Wolke besorgt man sich in einer Apotheke Bärlappsporen (Lycopodiumpulver) und stäubt diese auf eine Glasscheibe. Die Scheibe wird dann von hinten beleuchtet mit Licht unterschiedlicher Farben. Genügend monochromatisches Licht geben LED-Lampen ab – ich habe eine Mini-Taschenlampe mit roter LED benutzt (deren eigentlicher Zweck es ist, nachts beim Sternegucken das zum Einstellen benötigte Licht zu liefern, weil rotes Licht die Dunkeladaption des Auges nicht behindert) sowie die blaue LED, die sich als Betriebsleuchte an meiner externen Festplatte befindet; als letztes zum Vergleich eine Mini-Taschenlampe mit weißer LED. Alle Lampen habe ich mit Aluminiumfolie umwickelt, in die ich mit einer Nadel ein Loch als Blende gestochen habe. (Der Knopf zum Anschalten rastet bei einigen Mini-Taschenlampen nicht ein – er lässt sich aber mit Klebefilm fixieren.) Dann habe ich nacheinander mit allen drei Lampen die Beugungsringe erzeugt und fotografiert. Ein kleiner Nachteil war, dass der Fotoapparat für rotes Licht empfindlicher ist, weshalb dieses Foto sehr viel heller ist. (Während der rote zweite Ring in Abbildung 4 deutlich zu sehen ist, kann man den blauen zweiten Ring nur mit Mühe erkennen; in Realität war der Unterschied nicht so groß.) Als letzten Schritt habe ich die Bilder zum direkten Vergleich in ein Bild kopiert.
- Abb. 13 ¦ Wellenlänge und Ringdurchmesser

-
Mithilfe von Bärlappsporen erzeugte Koronen bei unterschiedlichen Wellenlängen; blaue LED, rote LED und weiße LED.
Man erkennt, dass der Außenrand des roten Hauptmaximums weiter außen liegt als der des blauen. Entsprechend überlagern sich über die komplette Ausdehnung des blauen Hauptmaximums alle Farben zu weiß. Der Rand des Hauptmaximumx bleibt rot, weil das blaue Hauptmaximum hier nicht mehr „hinreicht“. Das erklärt den gelb-rötlichen Rand der Aureole.
Einfluss der Tropfengröße
Der Durchmesser der Ringe ist auch von der Größe des beugenden Hindernisses abhängig, im Fall der Korona also von der Größe der Wassertropfen in den Wolken. Große Tropfen erzeugen kleine Koronen, kleine Tropfen erzeugen weite Koronen. Je größer also eine Korona ist, aus desto kleineren Tropfen besteht die Wolke, durch die das Licht hindurchgeht. Mithilfe von Gleichung (1) lässt sich die Abhängigkeit der Intensitätsverteilung von der Tropfengröße darstellen. Für blaues Licht (440 nm) findet sich das 1. Minimum für einen Tropfenradius von 10 μm bei ca. 1,5°, für einen Tropfenradius von 20 μm bei ca. 0,8°.
Nicht nur der Radius der Ringe nimmt mit abnehmender Tropfengröße zu, auch der Abstand der Maxima bzw. Minima zueinander und damit die Breite der Ringe. Der Winkelunterschied zwischen Rot (650 nm) und Blau (440 nm) im 1. Nebenmaximum beträgt für einen Tropfenradius von 10 μm beispielsweise etwa 0,7°, bei 20 μm nur etwa 0,3° (berechnet mit Gleichung (1)).
- Abb. 14 ¦ Einfluss der Tropfengröße
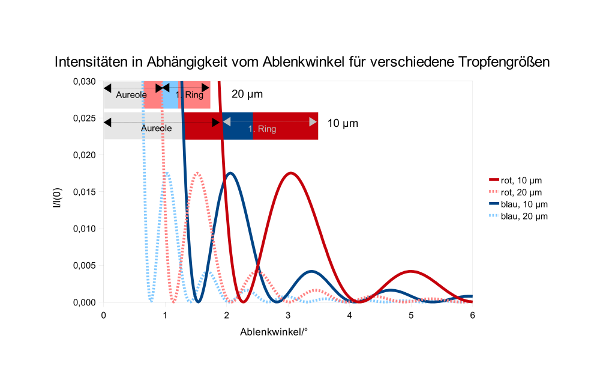
- Die Intensitäten in Abhängigkeit vom Ablenkwinkel für verschiedene Tropfengrößen. Kräftiges Rot und Blau entspricht der Beugung an einem 10-μm-Tropfen, helle Farben einer Beugung an 20-μm-Tropfen.
Die Mond- und die Sonnenscheibe sind keine punktförmigen Lichtquellen, sondern haben einen Winkeldurchmesser von etwa 0,5°, weshalb das von ihnen ausgesandte Licht nicht wirklich parallel ist. Das führt zu einer Verschmierung der Ringe, die sich umso deutlicher bemerkbar macht, je geringer die Farbaufspaltung ist. Da andererseits die Farbaufspaltung umso kleiner ist, je größer die Tropfen sind, sind für Tropfen mit Radien größer als etwa 30 μm keine Ringstrukturen mehr zu erkennen.
Zu kleine Tropfen (weniger als 5 μm Radius) dagegen beugen das Licht in einen großen Winkel und erzeugen breite Ringe, weshalb die Intensität entsprechend sinkt und der Kontrast und damit die Sichtbarkeit gegenüber dem Hintergrund abnimmt.
Die Tropfengröße darf nicht zu unterschiedlich sein – da jede Tropfengröße ihre eigenen Ringdurchmesser erzeugt, fallen bei einer zu breiten Verteilung der Tropfengröße schließlich Ringe unterschiedlicher Farben übereinander und das Ringmuster verschwindet. Da die Tropfengröße in Wolken aber nie völlig einheitlich ist, kommt es immer zu Überlagerungen verschiedener Farben. Die Farben in Koronen sind deshalb keine reinen Farben.
Ändert sich die Tropfengröße im Laufe der Zeit, ändert sich entsprechend auch die Ausdehnung der Ringe. Nähert sich beispielsweise ein Regengebiet, wachsen die Tropfen rasch und die Korona wird enger. Da die Tropfengröße auch uneinheitlicher wird, verschwinden die farbigen Ringe und die Korona geht in eine weiße Scheibe über.
Kann man nur die Aureole beobachten, haben die Tropfen in der Wolke daher meistens eine uneinheitliche Größe. Da solche Wolken häufiger sind als solche mit einheitlicher (und passender) Tropfengröße, sind nur aus Aureolen bestehende Koronen häufiger zu beobachten als solche mit farbigen Ringen.
- Abb. 15 ¦ Tropfengröße und Koronaform

- Abweichungen von der Kreisform kommen zustande, wenn verschiedene Bereiche der Wolken unterschiedlich große Tropfen enthalten.
Bestimmung der Tropfengröße aus dem Ringradius
Mithilfe von Gleichung (1) lässt sich die Position des 1. Minimums bestimmen. Ein Minimum der Intensität ist in Gleichung (1) gleichbedeutend mit einer Nullstelle der Besselfunktion J1(x). Deren erste Nullstelle für x > 0 liegt bei x = 3,38, sodass gilt:
x = (2π / λ) R sin θ = 3,83
Gleichung (1) lässt sich dann vereinfachen zu:
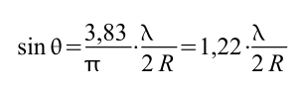 (2)
(2)
In der Gleichung sind: θ = Winkelposition des 1. Minimums; λ = Wellenlänge des gebeugten Lichtes; R = Radius des Tropfens.
Aufgelöst nach dem Tropfendurchmesser ergibt sich: 2R = 1,22 (λ /sin θ)
Über diese Gleichung lässt sich aus dem Ringdurchmesser die Größe der verursachenden Tropfen abschätzen. Die äußeren Ränder der roten Ringe liegen etwa an der Position der gelben Minima, wie bereits Joseph Fraunhofer herausfand. Löst man also Gleichung (2) nach dem Tropfendurchmesser 2R auf, setzt λ = 571 nm (gelbes Licht) und bestimmt die Winkelausdehnung θ des roten Randes der Aureole einer beobachteten Korona, erhält man eine Abschätzung für die Größe der Tropfen, die diese Korona erzeugt haben.
Ein praktisches Problem ist dabei die Bestimmung der Winkelausdehnung θ einer beobachteten Korona. Eine Möglichkeit, dieses Problem zu lösen, besteht darin, die Ausdehnung der Korona mit derjenigen der Mondscheibe zu vergleichen, die etwa 0,5° beträgt. Im abgebildeten Foto wurde die bei derselben Brennweite aufgenommene Mondscheibe in die Korona hineinkopiert (und schwarz eingefärbt). Die Ausdehnung des ersten roten Ringes lässt sich durch Ausmessen nun auf einen Wert von etwa 3,3° abschätzen. (Zu beachten ist, dass der Ablenkwinkel nur der Hälfte des Ringdurchmessers entspricht, also etwa 1,7°.) Daraus ergibt sich ein Tropfenradius von etwa 12 μm.
- Abb. 16 ¦ Abschätzung der Tropfengröße

- Mondkorona, in die die bei derselben Brennweite aufgenommene Mondscheibe (schwarz eingefärbt) hineinkopiert wurde.
Simulationen
Einfluss von Tropfengröße und Wellenlänge
Anhand von Simulationen von Koronen kann man zeigen, wie sich die Größe des beugenden Gegenstandes und die Wellenlänge auswirken. Unter http://www.atoptics.co.uk/droplets/iris.htm gibt es das frei verfügbare Simulationsprogramm IRIS (Autor: Les Cowley) zum Berechnen von (unter anderem) Koronen. (Darüberhinaus bietet die Seite auch beeindruckende Fotos von Koronen und anderen Leuchterscheinungen der Atmosphäre.) Wir hatten schon festgestellt, dass Beugungserscheinungen umso stärker auftreten, je kleiner der beugende Gegenstand im Vergleich zur Wellenlänge ist. Kleine Tropfen beugen das Mondlicht daher stärker als große – das heiß, sie erzeugen größere Ablenkwinkel, also Ringe mit größeren Radien. Lange Wellen werden stärker gebeugt als kurze – die roten Ringe liegen also weiter außen als die blauen.
- Abb. 2 ¦ Einfluss der Tropfengröße – Simulation

-
Simulationen von Koronen bei unterschiedlichen Tropfengrößen. Links: Tropfenradius 20 μm; rechts: Tropfenradius 5 μm. Die Radien der Beugungsringe sind für die kleinen Tropfen wie erwartet größer als für die großen.
Es handelt sich um Simulationsrechnungen, durchgeführt mit dem Programm IRIS (© 2002, Les Cowley; unter: http://www.atoptics.co.uk/droplets/iris.htm).
Dieses Bild darf kopiert, aber nicht verändert werden.
- Abb. 3 ¦ Einfluss der Wellenlänge – Simulation

-
Simulationen von Koronen bei unterschiedlichen Wellenlängen. Unten links für blaues (440 nm), unten rechts für rotes (650 nm) Licht, oben für Sonnenlicht. Die Radien der Beugungsringe des roten Lichtes sind wie erwartet größer als die der blauen Ringe.
Es handelt sich um Simulationsrechnungen, durchgeführt mit dem Programm IRIS (© 2002, Les Cowley; unter: http://www.atoptics.co.uk/droplets/iris.htm). Tropfenradius: 5 μm.
Dieses Bild darf kopiert, aber nicht verändert werden.
Stark unterschiedliche Tropfengrößen innerhalb einer Wolke
Da Wolken nie aus Tropfen einer einheitlichen Größe bestehen, verschwimmen die farbigen Ringe mehr oder weniger. Jede Tropfengröße erzeugt ihre eigenen Beugungsringe, die sich überlagern. Die Farben vermischen sich dann und die Ringe verschmieren.
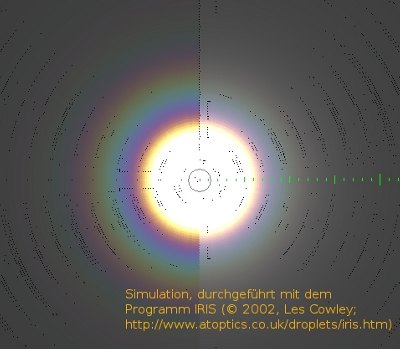
- Abb. 5 ¦ Einfluss der Verteilung der Tropfengröße – Simulationen
-
Simulation von Koronen bei uneinheitlicher Tropfengröße. Der mittlere Tropfenradius beträgt 12 μm; links: Standardabweichung 5 %; rechts: Standardabweichung 20 %. (Eine größere Standardabweichung bedeutet, dass die Tropfengröße weniger einheitlich ist.) Es handelt sich um Simulationsrechnungen, durchgeführt mit dem Programm IRIS (© 2002, Les Cowley; unter: http://www.atoptics.co.uk/droplets/iris.htm).
Dieses Bild darf kopiert, aber nicht verändert werden.
Koronen und das Wetter
Ausgeprägte Koronen treten auf, wenn sich in großen Höhen Schichtwolken aus kleinen Wassertröpfchen bilden – Altocumulus oder Cirrocumulus. Da die meisten Koronen durch Beugung an Wassertropfen entstehen, Wolken aus Wassertropfen aber oftmals entweder gar keinen oder nur Nieselregen bringen, entstanden Bauernregeln wie diese:
Ist der Ring nahe Sonne oder Mond,
uns der Regen verschont,
ist der Ring aber weit,
hat er Regen im Geleit.
Die zweite Hälfte dieser Regel beziehen sich auf den Halo, der zum einen weiter ist als eine Korona und leichter um die Sonne beobachtet werden kann als die Korona und seltener um den Mond. Ein Halo entsteht in dünnen hohen Eiswolken (Cirrostratus), die zu den Vorboten eines Sturmtiefs gehören.
Niederschläge entstehen (in unseren Breiten) überwiegend aus Wolken, in denen Wassertropfen und Eiskörner gleichzeitig vorliegen. In dem Fall können aufgrund des unterschiedlichen Dampfdrucks die Eiskörner auf Kosten der Wassertropfen sehr rasch wachsen und so die zum Fallen nötige Größe erreichen (siehe Sättigungsampfdruck über Eis und über Wasser).
© Wiebke Salzmann, August 2013
