Dr. Wiebke Salzmann
freie Lektorin und Autorin
Wissenstexte
Physik-Wissen
Entropie I

Die Entropie eines abgeschlossenen Systems verringert sich nicht von allein.
www.wissenstexte > Physik-Wissen > Thermodynamik > Entropie I
Entropie I
– Reversible und irreversible Prozesse
– Entropie und 2. Hauptsatz der Thermodynamik
– Entropie und Unordnung
– Perpetuum mobile
– Gefrieren und Entropie
– Geschichte: Paradiesische Zustände (Link)
– Geschichte: Das Paradies bleibt geschlossen (Link)
– Geschichte: Aber wenigstens der Tee ist süß und nicht zu heiß (Link)
1. und 2. Hauptsatz der Thermodynamik – Grenzen der Energieumwandlung
Dieselbe Energie immer wieder verwenden zu können – das wäre schön. Man könnte die Heizwärme gewissermaßen wieder einsammeln und den Raum erneut damit heizen. Aber wir wissen, dass das nicht geht und dass jedes Jahr eine neue Gasrechnung kommt.
Der erste Hauptsatz der Thermodynamik – der Energieerhaltungssatz – legt nur die „Gesamtbilanz“ fest, also die Tatsache, dass die Gesamtenergie eines abgeschlossenen Systems nicht zu- oder abnehmen darf. Er verbietet, dass Energie aus dem Nichts erzeugt werden kann (oder dahin verschwinden) und dass Arbeit verrichtet werden kann, ohne dass Energie dazu verwendet wird. Dagegen bestimmt der zweite Hauptsatz der Thermodynamik, in welchem Ausmaß sich welche Energieformen wie ineinander umwandeln können und welche Prozesse spontan ablaufen. Thermische Energie kann nicht vollständig in andere Energieformen umgewandelt werden, es wird immer ein Rest Wärme ungenutzt an die Umgebung abgegeben. Die Wärme, die einer Dampfmaschine zugeführt wird, kann nicht vollständig in mechanische Energie der Kolbenbewegung umgewandelt werden, ein Teil „verpufft“ ungenutzt an die Umgebung.
Hier finden Sie eine Geschichte zum 1. Hauptsatz der Thermodynamik
Reversible und irreversible Prozesse
Zunächst denkt man bei den Energieverlusten an die Verluste durch Reibung. Fällt zum Beispiel ein ideal elastischer Ball auf den Boden, springt er wieder hoch. Da es sich um einen ideal elastischen Ball handelt, bleibt seine mechanische Energie (also die Summe aus potenzieller und kinetischer Energie) erhalten – das heißt, er wird nach dem Aufprall wieder auf die Höhe, die er zu Beginn des Falles hatte, zurückspringen. Erhaltung der mechanischen Energie bedeutet, es gibt keine Verformungen oder Reibung, also keine Vorgänge, bei denen Wärme erzeugt würde. Damit ist der gesamte Vorgang reversibel. Würde man den Fall des Balles und das anschließende Hochspringen filmen, könnte man keinen Unterschied zwischen dem vorwärts und dem rückwärts laufenden Film erkennen. Nun gibt es in der Realität aber keine ideal elastischen Bälle. Bei einem echten Ball wird bei jedem Aufprall Bewegungsenergie in Wärme umgewandelt – durch Reibung zwischen Ball und Boden aber auch im Ball selbst bei seiner Verformung – und geht für weitere Bewegungen somit verloren. Mit jedem erneuten Hochspringen ist die erreichte Höhe deshalb geringer als die vorherige. Würde man einen solchen Prozess filmen, könnte man ohne weiteres zwischen dem vorwärts und dem rückwärts abgespulten Film unterscheiden. Der reale Prozess ist also unumkehrbar oder auch irreversibel.
In der Natur sind alle Vorgänge irreversibel. Trotzdem nutzt man in Gedankenexperimenten gelegentlich auch reversible Prozesse. Ein solches Gedankenexperiment ist der carnotsche Kreisprozess, bei dem eine Maschine in vier reversibel durchlaufenen Schritten Wärme aus einem Wärmespeicher hoher Temperatur entnimmt und Arbeit gewinnt. Allerdings kann nicht die gesamte aufgenommene Wärme in Arbeit umgewandelt werden. Ein Teil Wärme wird ungenutzt an einen zweiten Wärmespeicher geringerer Temperatur abgegeben.
Also gilt bereits für reversible Vorgänge, dass Wärme nicht vollständig in Arbeit umgewandelt werden kann – also auch dann nicht, wenn keine Reibungsverluste auftreten!
Bei irreversibel arbeitenden Maschinen ist die aus der Wärme erhaltene Arbeit noch kleiner, es geht aufgrund der Reibungs- oder Strahlungsverluste noch mehr Wärme ungenutzt verloren, als bei einer reversibel arbeitenden.
Die exakte Formulierung des zweiten Hauptsatzes der Thermodynamik lautet: Es ist nicht möglich, eine periodisch arbeitende Maschine zu bauen, deren einzige Wirkung darin besteht, eine mechanische Arbeit zu verrichten und einen Wärmespeicher abzukühlen. (Eine periodisch arbeitende Maschine wäre zum Beispiel so ein Kreisprozess wie der carnotsche Kreisprozess.)
Eine zweite Formulierung des zweiten Hauptsatzes kennen wir schon aus dem Alltag: Wärme kann nicht von selbst von einem kälteren auf einen wärmeren Körper übergehen. Eine Tasse Tee wird sich von allein immer abkühlen und niemals Wärme aus der Luft aufnehmen und heißer werden. Würde Wärme von selbst von einem kälteren auf einen wärmeren Körper übergehen, könnte man beispielsweise die thermische Energie der Ozeane nutzen und hätte eine quasi unerschöpfliche Energiequelle.
Entropie und der zweite Hauptsatz der Thermodynamik
Führt man einem System Wärme (Q) zu, erhöht das auch seine Entropie (S). Für reversible Prozesse gilt:
dS = dQreversibel / T,
das heißt, die Entropieänderung dS ist proportional zur zu- oder abgeführten Wärme dQ und umgekehrt proportional zu der Temperatur T, bei der das geschieht. Je mehr Wärme zugeführt wird, desto stärker erhöht sich die Entropie des Körpers. Führt man einem kalten Körper dieselbe Menge Wärme zu wie einem warmen, erhöht sich die Entropie im kalten Körper stärker.
Tritt nun in einem irreversiblen Prozess auch noch Reibungswärme auf, verursacht dies eine zusätzliche Entropiezunahme. Damit ist die gesamte Entropiezunahme größer (beziehungsweise bei Wärmeabfuhr die gesamte Entropieabnahme kleiner) als im reversiblen Fall und die Gleichung wird zu:
dS > dQreversibel / T.
Betrachten wir nun ein thermisch abgeschlossenes System, findet kein Wärmeaustausch mit der Umgebung statt und dQ ist null. Damit wird für reversible Prozesse dS = 0, für irreversible, also reale, Prozesse gilt: dS > 0.
Dies ist eine dritte – und die vielleicht bekannteste – Formulierung des 2. Hauptsatzes der Thermodynamik:
Die Entropie eines abgeschlossenen Systems verringert sich nicht von allein.
Das bedeutet, dass die Entropie sich in abgeschlossenen Systemen überhaupt nicht verringern kann – denn eine Abnahme der Entropie in einem System kann nur durch eine Einwirkung von außen erzwungen werden, und das ist bei abgeschlossenen Systemen ja gerade ausgeschlossen.
Bei reversiblen Vorgängen, bei denen also keine Reibungswärme entsteht, bleibt die Entropie in abgeschlossenen Systemen konstant. Da es aber in der Realität keine reversiblen Vorgänge gibt, ist dieser Fall recht theoretisch. Bei allen realen Vorgängen kann die Entropie in abgeschlossenen Systemen von allein nur zunehmen.
In abgeschlossenen Systemen können nur spontane, also von allein ablaufende Prozesse stattfinden – Einwirkung von außen ist ja ausgeschlossen. Spontan können nach dem zweiten Hauptsatz aber nun nur solche Prozesse ablaufen, bei denen die Entropie zunimmt; und das tut sie so lange, bis ein Gleichgewicht erreicht ist und der Prozess zum Stillstand kommt. Dann hat die Entropie ihren maximalen Wert. Anschließend passiert gar nichts mehr – und wenn keine Vorgänge stattfinden, ändert sich auch die Entropie nicht.
Mit dem 2. Hauptsatz wird also festgelegt, in welche Richtung Prozesse spontan ablaufen – nämlich in diejenige zunehmender Entropie. Die Umkehrung dieser Prozesse findet nicht von allein statt. Deshalb kann man erkennen, ob ein Film vorwärts oder rückwärts läuft – auf die Weise erzeugt die Entropie eine Zeitachse.
Entropie und Unordnung
Die etwas laxe Art, Entropie umgangssprachlich mit Unordnung gleich zu setzen, ist etwas problematisch. Anschaulich ist zwar gut vorstellbar, dass ein Gas, in dem die Teilchen wild durcheinanderfliegen, unordentlicher ist als ein Kristall, in dem die Teilchen fest auf ihren Gitterplätzen sitzen. Darum geht es bei der Entropie jedoch eigentlich nicht.
- Abb. 1a ¦ Jugendfeuerwehr mit niedriger Entropie

- Es gibt viel weniger Möglichkeiten, die Jugendfeuerwehrmitglieder des Landkreises Rostock in der Formation „JF LRO“ aufzustellen …
- Abb. 1b ¦ Jugendfeuerwehr mit hoher Entropie
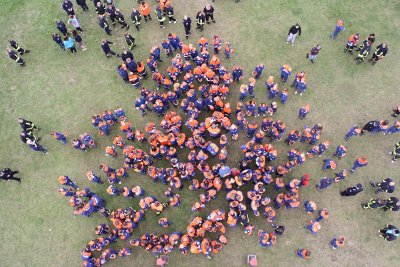
- … als sie alle durcheinanderlaufen zu lassen. Deshalb hat dieser Zustand eine viel höhere Entropie als der im oberen Bild (Erklärung im folgenden Text).
Die Fotos entstanden bei dem jährlich stattfindenden Wettbewerb „Spiele ohne Grenzen“ der Jugendfeuerwehren des Landkreises Rostock. (Quelle: Kreisfeuerwehrverband Landkreis Rostock)
Während es (stark vereinfacht dargestellt) bei einem Kristall am absoluten Temperaturnullpunkt, also ohne Wärmebewegung der Teilchen (wie Kinder, die steif auf ihren Stühlen sitzen, weil vorn der strenge Mathe-Lehrer steht), nur eine Möglichkeit gibt, die Teilchen anzuordnen, gibt es für einen Kristall bei höherer Temperatur, wenn die Teilchen zwar auch feste Plätze haben, sich auf diesen aber hin und her bewegen können (wie Kinder, die auf ihren Stühlen kippeln und zappeln), schon sehr viele Möglichkeiten, wie die Teilchen zueinander liegen können – mal sind die einen etwas nach links ausgelenkt, mal die anderen etwas nach oben. Von unserer Warte aus betrachtet, also makroskopisch (d. h., die einzelnen Teilchen sind nicht erkennbar), sehen alle diese Zustände jedoch gleich aus. In einer Flüssigkeit gibt es noch weit mehr Möglichkeiten, die Teilchen anzuordnen, da sie sich umeinander bewegen können, wenn sie auch soweit aneinander gebunden sind, dass sie die Flüssigkeit nicht verlassen können (die Kinder laufen jetzt frei im Klassenraum herum, dürfen diesen aber nicht verlassen) – und auch diese vielen Möglichkeiten sehen für uns alle gleich aus. Obwohl mikroskopisch natürlich auch jede einzelne Anordnung der Flüssigkeitsteilchen für sich genauso einzigartig ist wie die regelmäßige Anordnung im Kristall! Wenn Sie ein Glas Wasser betrachten, sieht es immer gleich aus – trotzdem wandern die Moleküle des Wassers herum und auf Teilchenebene sieht jede Momentaufnahme des Wassers anders aus.
Nehmen wir einmal an, es gäbe nur eine einzige Möglichkeit, einen Kristall aus den Teilchen zusammenzusetzen, und es gäbe eine Million Möglichkeiten, wie die Teilchen sich in der Flüssigkeit anordnen könnten. (In Wirklichkeit sind es natürlich viel mehr.) Insgesamt gibt es also eine Million und eine Möglichkeit, die Teilchen anzuordnen. Die Wahrscheinlichkeit für jeden einzelnen Zustand beträgt demnach 1 : 1.000.001. Aber die Wahrscheinlichkeit, überhaupt eine Flüssigkeit zu erhalten, setzt sich aus all den Wahrscheinlichkeiten für die Flüssigkeitszustände zusammen, beträgt also 1.000.000 : 1.000.001, und das ist beinah 1 oder 100 %. Die Wahrscheinlichkeit, einen Kristall zu erhalten, beträgt aber immer noch 1 : 1.000.001, da es hierfür nur einen Zustand gibt.
Makroskopisch steht also die eine Teilchenanordnung beim kalten Kristall den vielen, vielen bei der Flüssigkeit gegenüber. Wenn ein Haufen Teilchen also zufällig einen Zustand einnimmt, wird dies mit sehr viel höherer Wahrscheinlichkeit ein flüssiger sein als ein Kristall. Wenn man aus einem Sack mit 1.000.000 roten und einer grünen Socke zufällig und blind eine herausgreift, wird das auch ziemlich sicher eine rote sein.
- Abb. 2a ¦ Wasser

- Flüssiges Wasser hat eine höhere Entropie …
- Abb. 2b ¦ Eis

- … als Eis.
Hier finden Sie eine Geschichte zum 2. Hauptsatz der Thermodynamik
Perpetuum mobile
Die Unmöglichkeit, ein Perpetuum mobile zu bauen, ist die Folge der ersten beiden Hauptsätze der Thermodynamik. Man unterscheidet zwischen dem Perpetuum mobile erster und dem zweiter Ordnung. Ein Perpetuum mobile erster Ordnung ist eine Maschine, die ohne Energiezufuhr Arbeit verrichten kann, also Energie „aus dem Nichts“ erzeugt und somit dem ersten Hauptsatz widerspricht. Ein Perpetuum mobile zweiter Art ist mit dem Energieerhaltungssatz durchaus vereinbar – es ist eine Maschine, die mechanische Arbeit erzeugt, indem sie einen Wärmespeicher abkühlt, ihm also Wärme entzieht und diese Wärme vollständig in Arbeit umwandelt. Energetisch ist dies nicht verboten – der erste Hauptsatz verbietet nicht, dass sich plötzlich alle Teilchen eines Körpers in dieselbe Richtung bewegen und den Körper aufsteigen lassen. Da es nun keine ungeordnete Teilchenbewegung in dem Körper mehr gibt, hat er keine thermische Energie mehr – diese hat er zunächst als kinetische und nach dem Aufsteigen als potenzielle Energie. Thermische Energie wäre demnach also vollständig in potenzielle Energie umgewandelt. Anders ausgedrückt hätte sich die Entropie der ungeordneten Teilchenbewegung auf die geringere Entropie der geordneten Teilchenbewegung verringert. Diesem Perpetuum mobile widerspricht aber der zweite Hauptsatz, der verbietet, dass Wärme vollständig in Arbeit umgewandelt wird.
Gefrieren und Entropie
Aber was ist, wenn man ein Glas Wasser in den Gefrierschrank stellt? Das gefriert ja dann trotzdem – allen Wahrscheinlichkeiten zum Trotz.
Zunächst einmal ist dieses Glas Wasser kein abgeschlossenes System. Des weiteren ändert sich bei der Bildung eines Eiskristalles nicht nur die Entropie, sondern auch die innere Energie (durch das Bilden von chemischen Bindungen zwischen den Wassermolekülen). Dieser Aspekt wurde bislang völlig ausgespart. Das Wasser hat nun wie jedes System das Bestreben, seine innere Energie möglichst klein zu machen. Legt man einen Ball an einen Hang, rollt er hinunter, weil im Tal seine potenzielle Energie geringer ist als auf der Höhe. Wasser gibt beim Gefrieren Schmelzwärme ab, hat also gefroren eine geringere innere Energie.
Schmelzwärme abgeben kann es aber nur, weil das Glas eben kein abgeschlossenes System ist. Wäre es abgeschlossen, könnte es die Wärme nicht abgeben und das Wasser könnte nicht in den gefrorenen Zustand übergehen. (Die innere Energie bleibt nach dem ersten Hauptsatz der Thermodynamik in abgeschlossenen Systemen bekanntlich konstant.) Und dann – wenn also das Wasser im flüssigen Zustand bleibt – ist es sehr, sehr unwahrscheinlich, dass sich alle Wassermoleküle an Positionen setzen, die denen in einem Eiskristall entsprechen.
Ob eine Reaktion oder auch eine Phasenumwandlung wie die von Wasser zu Eis spontan abläuft oder nicht, wird in offenen Systemen also von zwei Größen bestimmt – innerer Energie und Entropie. Energieabgabe und Entropiezunahme begünstigen eine spontane Reaktion, Energieaufnahme und Entropieabnahme stehen ihr entgegen. Wird Energie vom System abgegeben und nimmt die Entropie gleichzeitig zu, läuft die Reaktion auf jeden Fall spontan ab. Es kann aber auch sein, dass zwar die Entropie abnimmt, aber so viel Energie abgegeben wird, dass die Reaktion trotzdem spontan abläuft, oder aber die Entropiezunahme ist so groß, dass auch eine Energie verbrauchende Reaktion freiwillig abläuft.
Bei Wasser über dem Gefrierpunkt ist es also die Entropie des Wassers, die sich durchsetzt und den flüssigen Zustand herbeiführt, unter dem Gefrierpunkt ist es die innere Energie des Wassers, die auf Kosten einer kleineren Entropie ein Minimum einnimmt und zum Gefrieren führt.
Trotzdem widerspricht das Gefrieren natürlich nicht dem zweiten Hauptsatz: Wenn Wasser gefriert, dann nimmt zwar dessen Entropie ab, aber wir müssen das Gesamtsystem aus Wasser und Umgebung betrachten. Beim Gefrieren gibt das Wasser Wärme an die Umgebung ab, die dort die Entropie erhöht. So dass wir in der Summe eine Entropieerhöhung erhalten.
© Wiebke Salzmann, April 2009
